Question

Help me with this question please and thank you!! :)

Answer 1

Question 1

The complement of set B is all the elements in S but that are not in B, which is
`\{2, 4, 5, 9, 10, 11, 12, 13, 14, 17, 19\}`.

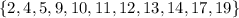We want to find the intersection of set A and the complement of set B, which is the set of all elements that both sets contain.

This is {2, 9, 10, 12}, meaning there are 4 elements.

Question 2

Following a similar logic as the last problem, the complement of set A is
`\{1,3,4,5,6,7,11,13,14,15,17,18,19\}`.

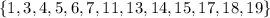Therefore, the desired set is
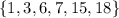`\{1,3,6,7,15,18\}`, and thus there are 6 elements.