Answer:
The new volume will be approximately 2.49 L.
Step-by-step explanation:
We are given that a gas sample occupies 4.39 L at 44° C.
We are also given that we are going decrease the temperature to 25° C.
Charles' Law has a formula which shows the relationship between the volumes of a samples and the temperatures of the samples.
The proportion is shown as:
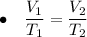 ,
,
where V₁ and V₂ are the initial and final volume respectively and T₁ and T₂ are the initial and final temperature respectively.
This proportion can be used to determine what our unknown is. We need to know the final volume.

Therefore, if we reduce the temperature to 25 °C, we will be reducing the volume of the substance to 2.49 L.