Answer:
One convergence criteria that is useful here is that, if aₙ is the n-th term of this sequence, then we must have:
Iaₙ₊₁I < IaₙI
This means that the absolute value of the terms must decrease as n increases.
Then we must have:
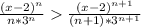
We can write this as:

If we assume that n is a really big number, then:
n + 1 ≈ 1
And we can write:
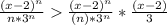
Then we have the inequality
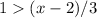
And remember that this must be in absolute value, then we will have that:
-1 < (x - 2)/3 < 1
-3 < x - 2 < 3
-3 + 2 < x < 3 + 2
-1 < x < 5
The first option looks like this, but it uses the symbols ≤≥, so it is not the same as this, then the correct option will be the second.