Answer: 491,891,400
Delete the commas if necessary.
============================================================
Step-by-step explanation:
There are 6 freshmen total and we want to pick 2 of them, where order doesn't matter. The reason it doesn't matter is because each seat on the committee is the same. No member outranks any other. If the positions were labeled "president", "vice president", "secretary", etc, then the order would matter.
Plug n = 6 and r = 2 into the nCr combination formula below
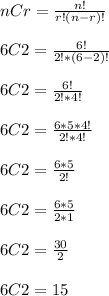
This tells us there are 15 ways to pick the 2 freshmen from a pool of 6 total.
Repeat those steps for the other grade levels.
n = 13 sophomores, r = 5 selections leads to nCr = 13C5 = 1287. This is the number of ways to pick the sophomores.
You would follow the same type of steps shown above to get 1287. Let me know if you need to see these steps.
Similarly, 8C4 = 70 is the number of ways to pick the juniors.
Lastly, 14C3 = 364 is the number of ways to pick the seniors.
-----------------------------
To recap, we have...
- 15 ways to pick the freshmen
- 1287 ways to pick the sophomores
- 70 ways to pick the juniors
- 364 ways to pick the seniors
Multiply out those values to get to the final answer.
15*1287*70*364 = 491,891,400
This massive number is a little under 492 million.