Answer:
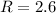
Explanation:
Given
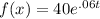
![[a,b] = [0,3]](https://img.qammunity.org/2021/formulas/mathematics/college/yyomhcllhi1myru5s9l8yu14ulz697whd9.png)
Required
Determine the average rate of change (R)
This is calculated as follows:
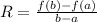
Where
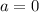 and
and

Substitute 0 for a and 3 for b
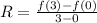
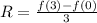
![R = (1)/(3)[f(3) - f(0)]](https://img.qammunity.org/2021/formulas/mathematics/college/jsdymgf0gyl5jtafjtam0zmkwl2od96svg.png)
Calculate f(3)
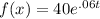
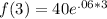
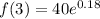

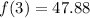
Calculate f(0)
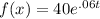


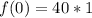
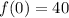
So, the expression:
![R = (1)/(3)[f(3) - f(0)]](https://img.qammunity.org/2021/formulas/mathematics/college/jsdymgf0gyl5jtafjtam0zmkwl2od96svg.png)
![R= (1)/(3)[47.88 - 40]](https://img.qammunity.org/2021/formulas/mathematics/college/t3xs6ks9kjxiulp7r0yv6l8gx2vsgdxci5.png)
![R= (1)/(3)[7.88]](https://img.qammunity.org/2021/formulas/mathematics/college/obrbc8mfndtcyo5k7vwdmajmxa3xya0u3c.png)
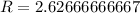
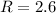
Hence, the average rate of change is approximately 2.6