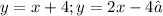The slope of both the lines are
 . Therefore, the correct option is B.
. Therefore, the correct option is B.
Line 1 (Passing through points
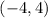 and
and
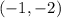 :
:
1. Calculate the slope (
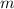 ) using the formula:
) using the formula:
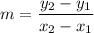
2. Substitute the coordinates of the two points into the formula:

3. Simplify the calculation:
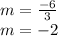
4. Use the point-slope form of the equation to get the equation of the line:

5. Choose one of the points for the equation, for example
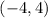 , and substitute the values:
, and substitute the values:
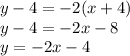
Line 2 (Passing through points
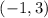 and
and
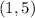 :
:
1. Calculate the slope
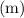 using the same formula as above.
using the same formula as above.
2. Substitute the coordinates of the two points into the formula:

3. Simplify the calculation:
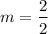
4. Simplify further to find the slope:
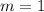
5. Use the point-slope form of the equation with one of the points, say
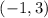 , and substitute the values:
, and substitute the values:
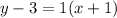
6. Distribute and rearrange to get the standard form or slope-intercept form:
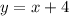
The correct options in the question are:
A.
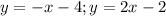
B.

C.
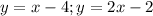
D.