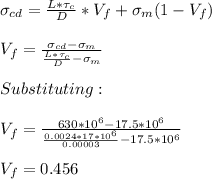Answer:
The answer is below
Step-by-step explanation:
Given that:
Diameter (D) = 0.03 mm = 0.00003 m, length (L) = 2.4 mm = 0.0024 m, longitudinal tensile strength
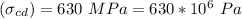 , Fracture strength
, Fracture strength
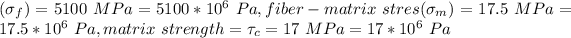
a) The critical length (
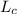 ) is given by:
) is given by:
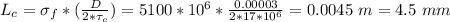
The critical length (4.5 mm) is greater than the given length, hence th composite can be produced.
b) The volume fraction (Vf) is gotten from the formula: