Explanation:
i = interest 3% for 30 years
This is a simple dynamical system for whom the the solutions are given as
](https://img.qammunity.org/2021/formulas/mathematics/college/8c5bwmd57h2of17yhscwec323olrvs598c.png)
putting values we get
S=2000[\frac{(1.03)^{30}-1}{0.03}](1.03)
= $98005.35
withdrawal of money takes place from one year after last payment
To determine the result we use the present value formula of an annuity date
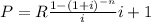
we need to calculate R so putting the values and solving for R we get
R= $6542.2356