Question

-

At x=3 the function given by f(x) {x^2, x>3
6x-9x>3
=

Answer 1

WHAT DOES THIS MEAN? I’m confused

Answer 2

At x = 3, the function given by
`f(x)=\left\{\begin{array}{Ir}x^2, & \text{if } x < 3\\6x-9, & \text{if } x \geq 3\end{array}\right` is: (C) both continuous and differentiable.

In Mathematics and Geometry, a continuous function is a type of function in which there is no discontinuities or breaks between the intervals for the points plotted on a graph.

Generally speaking, a function is said to be continuous at a given input value when the left-hand limit is equal to the right-hand limit;

`\lim_(x \to a^-) f(x)= \lim_(x \to a^+) f(x)`

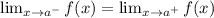
By critically observing the graph of the function f, we can logically deduce that the graph of f is continuous at x equals 3;

`\lim_(x \to 3^-) f(x)=9\\\\ \lim_(x \to 3^+) f(x)=9`

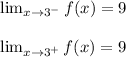
In order for any function to be differentiable at any point x = a in its domain, it must be continuous at the given point. By critically observing the graph of the function f(x), we can logically deduce that the graph of f(x) is continuous at x equals 3.

In conlusion, this function is both continuous and differentiable at x equals 3 because the right-hand and left-hand limit exist, as f(3) equals 9.

Complete Question:

At x = 3, the function given by
`f(x)=\left\{\begin{array}{Ir}x^2, & \text{if } x < 3\\6x-9, & \text{if } x \geq 3\end{array}\right` is:

(A) continuous but not differentiable.

(B) differentiable but not continuous.

(C) both continuous and differentiable.

(D) neither continuous nor differentiable.