Answer:
16π
Explanation:
Given that:
The sphere of the radius =
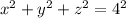

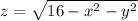
The partial derivatives of
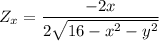
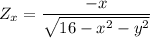
Similarly;
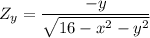
∴
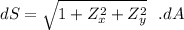
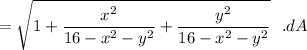
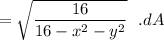
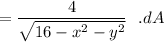
Now; the region R = x² + y² = 12
Let;
x = rcosθ = x; x varies from 0 to 2π
y = rsinθ = y; y varies from 0 to
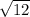
dA = rdrdθ
∴
The surface area
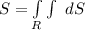

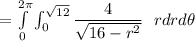

![= 2 \pi * 4 \Bigg [ (√(16-r^2))/((1)/(2)(-2)) \Bigg]^(√(12))_(0)](https://img.qammunity.org/2021/formulas/mathematics/college/m12mo191butks7f1no8zlpgmh6o4nlugof.png)
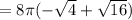
= 8π ( -2 + 4)
= 8π(2)
= 16π