Question

A steel wire in a piano has a length of 0.540 m and a mass of 4.800 ✕ 10−3 kg. To what tension must this wire be stretched so that the fundamental vibration corresponds to middle C (fC = 261.6 Hz on the chromatic musical scale)?

Answer 1

T = 708.81 N

Step-by-step explanation:

Given that,

Length of a steel wire in a piano, l =0.54 m

Mass,
`m=4.8* 10^(-3)\ kg`

We need to find the tension must this wire be stretched so that the fundamental vibration corresponds to middle C, fc = 261.6 Hz

The equation for fundamental frequency is given by :

`f=(1)/(2l)* \sqrt{(T)/(\mu)} \\\\f=(1)/(2l)* \sqrt{(T)/((m)/(l))} \\\\261.6=(1)/(2* 0.54)* \sqrt{(T)/((4.8* 10^(-3))/(0.54))} \\\\261.6* 2* 0.54=\sqrt{(T)/((4.8* 10^(-3))/(0.54))}\\\\282.528=\sqrt{(T)/(0.00888)} \\\\(282.528)^2=(T)/(0.00888)\\\\T=708.81\ N`

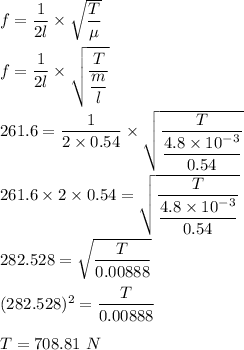
So, the required tension in the wire is 708.81 N.