Question

The standard deviation in a large population is equal to 8.3. How big sample is needed to be 90% sure that the sample mean is within 1.3units of the population mean?

Answer 1

111

Step-by-step explanation:

The sample mean is within 1.3units of the population mean, therefore the margin of error (E) = 1.3

confidence (C) = 90% = 0.9

α = 1 - C = 1 - 0.9 = 0.1

α/2 = 0.1 / 2 = 0.05

The z value for a confidence of 90% = z value of α/2 = z value of 0.45 (0.5 - 0.05) = 1.645

Given that E = 1.3, standard deviation (σ) and sample size = n.

The margin of error (E) is given by:

`E=Z_(\alpha)/(2)*(\sigma)/(√(n) ) \\\\Substituting:\\\\1.3=1.645*(8.3)/(√(n) )\\\\√(n)= 1.645*(8.3)/(1.3)\\\\√(n) =10.5\\\\n=110.3`

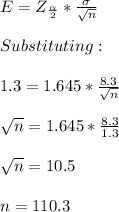
n ≈ 111 (to the next whole number)