Question

John gives 2/3 of his pencils, P, to Roy and then gives 1/4 of the pencils that he has left to Maria. In terms of P, how many pencils does john now have

a. 1/6

b. 1/3

c. 1/4

Answer 1

C. 1/4

Explanation:

Since John has given 2/3 of his pencils to Roy, he has 1/3 of the total left. To find 1/4 of 1/3, multiply the numbers. 1/4(1/3) = 1/12. This means that he gave 1/12 of the beginning total to Maria. 2/3 can also be written as 8/12, and 1 can be written as 12/12. 12/12 - 8/12 = 4/12, and then 4/12 - 1/12 = 3/12. 3/12 can be simplified into 1/4

Answer 2

John's remaining pencils in term of p = p/4

Hence, option 'c' is true.

Explanation:

Let 'p' be the total number of pencils

Given that John gives 2/3 of his pencils = 2/3 of p

= 2/3 × p

= 2/3 p

Pencils left:

`p-(2)/(3)p`

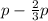
Factor out common term p

`p-(2)/(3)p=p\left(1-(2)/(3)\right)`

`=(1)/(3)p`

`=(p)/(3)`

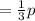
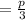
Pencils John gave to Maria = 1/4 × p/3 = p/12

The remaining Pencils in terms of 'p' =
`(p)/(3)-(p)/(12)`

`=(3p)/(12)`

`=(p)/(4)`

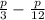
Thus, John's remaining pencils in term of p = p/4

Hence, option 'c' is true.