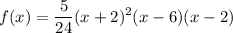Question

Please help me solve this...

Use the given information about a polynomial function to write the equation.
Degree 4. Root of multiplicity 2 at x=-2, and roots with multiplicity of 1 at x=6
and x=2. y-intercept at (0,10)

Answer 1

`\displaystyle f(x)=(5)/(24)(x+2)^2(x-6)(x-2)`

Explanation:

The standard, factored polynomial function is given by:

`f(x)=a(x-p)^n(x-q)^m...`

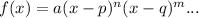
Where a is the leading coefficient,

p and q are factors,

And n and m are the powers or multiplicity they are being raised to.

We know that our polynomial function is of degree 4.

We have a root of multiplicity of 2 at x=-2.

So, our factor is:

`(x-(-2))=(x+2)\\`

It is has a multiplicity of 2, it is squared. So:

`(x+2)^2`

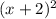
We have another root with multiplicity of 1 at x=6.

So, our factor is:

`(x-6)`

And since it is to the first power, we can write it as is.

Finally, we have another root of multiplicity of 1 at x=2.

So, our factor is:

`(x-2)`

Therefore, our entire function is:

`f(x)=a(x+2)^2(x-6)(x-2)`

We still have to determine our leading coefficient, a.

We can use that y-intercept. The y-intercept is at (0, 10). So, when x=0, y=10. By substitution:

`10=a(0+2)^2(0-6)(0-2)`

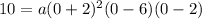
Evaluate:

`10=a(4)(-6)(-2)`

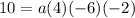
Multiply:

`10=48a`

Therefore:

`\displaystyle a=(10)/(48)=(5)/(24)`

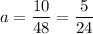
Therefore, our final function is:

`\displaystyle f(x)=(5)/(24)(x+2)^2(x-6)(x-2)`