Question

A spring is compressed by 0.0880 m and is used to launch an object horizontally with a speed of 2.76 m/s. If the object were attached

to the spring, at what angular frequency (in rad/s) would it oscillate?

Answer 1

Approximately
`3.14\; {\rm rad \cdot s^(-1)}`.

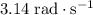Step-by-step explanation:

Fact: the angular velocity
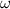`\omega` of a simple harmonic oscillator is the ratio between the maximum velocity
`v_{\text{max}}` and the maximum displacement
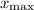`x_\text{max}` of this oscillator. In other words:

`\begin{aligned} \omega &= \frac{v_{\text{max}}}{x_{\text{max}}}\end{aligned}`.

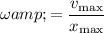Derivation of the previous equation:

Let
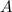`A` denote the amplitude of this oscillation, and let
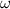`\omega` denote the angular velocity.

The displacement of the oscillator at time
`t` would be:

`x(t) = A\, \sin(\omega\, t)`.

The maximum displacement of this oscillator would be
`x_\text{max} = A`.

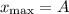The velocity of this oscillator at time
`t` is the derivative of displacement with respect to time:

`\begin{aligned} v(t) &= (d)/(d t)\, [x(t)] \\ &= (d)/(d t) [A\, \sin(\omega\, t)] \\ &= A\, \omega\, \cos(\omega\, t)\end{aligned}`.

The maximum velocity of this oscillator would be
`v_\text{max} = A\, \omega`.

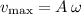Notice that dividing
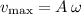`v_\text{max} = A\, \omega` by
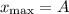`x_\text{max} = A` would give:

`\displaystyle \frac{v_\text{max}}{x_\text{max}} = (A\, \omega)/(A) = \omega`.

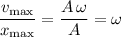It is given that
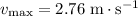`v_\text{max} = 2.76\; {\rm m\cdot s^(-1)}` while
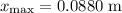`x_\text{max} = 0.0880\; {\rm m}`. Therefore:

`\begin{aligned} \omega &= \frac{v_{\text{max}}}{x_{\text{max}}} \\ &= \frac{2.76\; {\rm m\cdot s^(-1)}}{0.0880\; {\rm m}} \\ &\approx 3.14\; {\rm s^(-1)}\end{aligned}`.

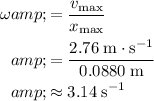(Radians per second.)