Problem 10
The two functions are inverses of each other. Why? Because we can think of f(x) = (x-7)/(-2) as y = (x-7)/(-2).
Swap x and y to get x = (y-7)/(-2). Solving for y leads to y = -2x+7 showing that g(x) = -2x+7 is the inverse of f(x) = (x-7)/(-2). This process can be done in reverse to get the same result.
===================================================
Problem 11
y = a(6)^(t/2)
y = a( 6^(1/2) )^t
y = a(2.4494897)^t
y = a( b )^t
where b = 6^(1/2) = 2.4494897 approximately
Set b equal to 1+r and solve for r
1+r = 2.4494897
r = 2.4494897-1
r = 1.4494897
This rounds to about r = 1.45
The r value is the decimal form of the percentage, which means we move the decimal point over two spots to the right to get 145% approximately
Answers:
The equation is roughly y = a(1 + 1.4494897)^t
The growth rate is approximately 145%
===================================================
Problem 12
You have the correct answer. Nice work.
===================================================
Problem 13
You are very close to the correct answer. However, you're missing the base of the log.
The answer should be
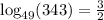 . So you'll need to write in a small "49" under the log.
. So you'll need to write in a small "49" under the log.
The general rule is that exponential equations in the form
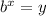 are equivalent to the log version of
are equivalent to the log version of
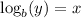 . For each equation, b is the base. The idea of logs is to isolate the exponent.
. For each equation, b is the base. The idea of logs is to isolate the exponent.