Question

11. rewrite the function in the form y=a (1+r)*

or y=a (1-r) ² then state the growth or decay
rate. y = a (6) t/a

Please help!!

Answer 1

Problem 10

The two functions are inverses of each other. Why? Because we can think of f(x) = (x-7)/(-2) as y = (x-7)/(-2).

Swap x and y to get x = (y-7)/(-2). Solving for y leads to y = -2x+7 showing that g(x) = -2x+7 is the inverse of f(x) = (x-7)/(-2). This process can be done in reverse to get the same result.

===================================================

Problem 11

y = a(6)^(t/2)

y = a( 6^(1/2) )^t

y = a(2.4494897)^t

y = a( b )^t

where b = 6^(1/2) = 2.4494897 approximately

Set b equal to 1+r and solve for r

1+r = 2.4494897

r = 2.4494897-1

r = 1.4494897

This rounds to about r = 1.45

The r value is the decimal form of the percentage, which means we move the decimal point over two spots to the right to get 145% approximately

Answers:

The equation is roughly y = a(1 + 1.4494897)^t

The growth rate is approximately 145%

===================================================

Problem 12

You have the correct answer. Nice work.

===================================================

Problem 13

You are very close to the correct answer. However, you're missing the base of the log.

The answer should be
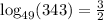`\log_(49)(343) = (3)/(2)`. So you'll need to write in a small "49" under the log.

The general rule is that exponential equations in the form
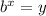`b^x = y` are equivalent to the log version of
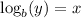`\log_(b)(y) = x`. For each equation, b is the base. The idea of logs is to isolate the exponent.