Answer: The perimeter of this triangle is 13.47.
Explanation:
First you should choose your first two points on the triangle that are on the same line. In this case I'll start with C = (3,3) and B = (8,6)
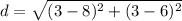
*Note: Keep X and Y consistent in the distance equation.
The distance for CB = 5.831
After finding this distance continue onto a new set of points to find a new length of the triangle, my second set of points will be A = (5,7) and B = (8,6) to find the length of AB.
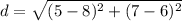
The distance for AB = 3.162
Now you're going to need to use your final to points, in this case for me A and C, and find the length of your final segment. So, I'll use point A = (5,7) and point C = (3,3).

The distance for AC =4.472
Then find the perimeter by adding up the three side lengths.
AB + CB + AC = P
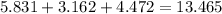
Finally, round 13.465 to the nearest hundredth, 13.47.
*Note: Make sure not to round your answer until the end of the problem to avoid less accurate or even wrong answers.