Question

1. Explain how to determine the equation of the function with

the following zeros. Be sure to explain each step as you show
how to determine the equation.
-5 multiplicity 2
-2 multiplicity 1

Answer 1

`P(x)=x^3+12x^2+45x+50`

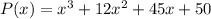
Explanation:

Roots of a polynomial

If we know the roots of a polynomial, say x1,x2,x3,...,xn, we can construct the polynomial using the formula

`P(x)=a(x-x_1)(x-x_2)(x-x_3)...(x-x_n)`

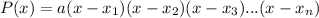
Where a is an arbitrary constant.

We are given the following roots:

-5 multiplicity 2 (-5 twice)

-2 multiplicity 1

Thus, the polynomial is:

`P(x)=a(x-(-5))(x-(-5))(x-(-2))`

`P(x)=a(x+5)(x+5)(x+2)`

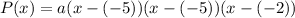
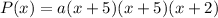
We are not given any clue about the value of a, so we choose a=1. Multiplying:

`P(x)=(x^2+5x+5x+25)(x+2)=(x^2+10x+25)(x+2)`

`P(x)=x^3+2x^2+10x^2+20x+25x+50`

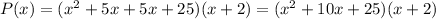
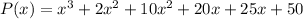
Simplifying:

`\mathbf{P(x)=x^3+12x^2+45x+50}`