The function represented by f(x) =
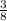
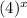 is an exponential function.
is an exponential function.
An exponential function is characterized by having a constant base raised to the variable power. In this case, the base is 4, and x is the exponent.
The coefficient
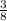 scales the function's output.
scales the function's output.
The general form of an exponential function is f(x)=a⋅
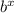 , where
, where
a is a constant multiplier, and
b is the base
So, the function f(x) =
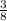
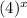 is a specific instance of an exponential function, where the base is 4, and the coefficient
is a specific instance of an exponential function, where the base is 4, and the coefficient
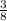 scales the exponential growth. Understanding these characteristics helps analyze the behavior of the function as x varies.
scales the exponential growth. Understanding these characteristics helps analyze the behavior of the function as x varies.