Question

A small sphere of mass 10 kg

is released from rest at a height of
15.0 m above the ground level.
The sphere experiences a constant
resistive force (due to air
resistance) of magnitude R = 10.0
N.
a) Calculate the speed of the
sphere after it has fallen
through a distance of 5.00 m

bCalculate the speed of the ball just before a it hits the gound.

Answer 1

Approximately
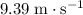`9.39 \; {\rm m\cdot s^(-1)}` after the sphere has travelled a distance of
`5\; {\rm m}`.

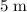Approximately
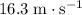`16.3\; {\rm m\cdot s^(-1)}` right before touching the ground (a distance of
`15\; {\rm m}`.)

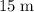Assumption:
`g = 9.81\; {\rm N\cdot kg^(-1)}`.

Step-by-step explanation:

Weight of the sphere:
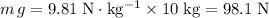`m\, g = 9.81\; {\rm N \cdot kg^(-1)} * 10\; {\rm kg} = 98.1\; {\rm N}`, downwards.

Drag on the sphere:
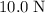`10.0\; {\rm N}` upwards.

Net force on the sphere:
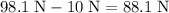`98.1\; {\rm N} - 10\; {\rm N} = 88.1\; {\rm N}` downwards.

Acceleration of the sphere:
`a = F_\text{net} / m = 88.1\; {\rm N} / (10\; {\rm kg}) = 8.81\; {\rm m\cdot s^(-2)}`.

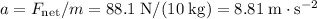Apply the SUVAT equation
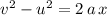`v^(2) - u^(2) = 2\, a\, x`, where
`v` is the final velocity,
`u` is the initial velocity (
`0` in this case, as the sphere was released from rest,) and
`x` is the distance (displacement) that the sphere has travelled so far.

Rearrange this equation to obtain an expression for
`v`:

`\displaystyle v = \sqrt{2\, a\, x + u^(2)}`.

For example, after the ball travelled a distance of
`5.00\; {\rm m}`,
`x = 5.00 \; {\rm m}`:

`\begin{aligned} v &= \sqrt{2\, a\, x + u^(2)} \\ &= \sqrt{2 * 8.81\; {\rm m\cdot s^(-2)} * 5.0\; {\rm m} + 0} \\ &\approx 9.39\; {\rm m\cdot s^(-1)}\end{aligned}`.

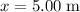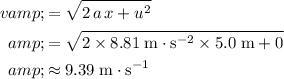Similarly,
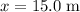`x = 15.0\; {\rm m}` right before landing, such that:

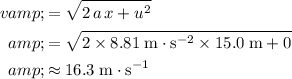`\begin{aligned} v &= \sqrt{2\, a\, x + u^(2)} \\ &= \sqrt{2 * 8.81\; {\rm m\cdot s^(-2)} * 15.0\; {\rm m} + 0} \\ &\approx 16.3\; {\rm m\cdot s^(-1)}\end{aligned}`.