Answer:
This equation illustrates the associative property of the real number field,
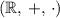 .
.
Explanation:
All four choices here are indeed properties of the field of real numbers,
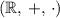 . However, the equation
. However, the equation
 makes use of only the associative property.
makes use of only the associative property.
Identity Property
By identity property of fields, the real number field
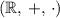 should contain an identity element
should contain an identity element
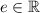 , such that for any element of that field
, such that for any element of that field
 :
:
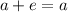 .
.
In particular, the identity element of the real number field
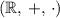 is the real number
is the real number
 . The identity property (of addition) would then read:
. The identity property (of addition) would then read:
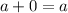 for any
for any
 .
.
Distributive Property
By the distributive property of fields, for any three elements (
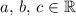 ) of the real number field
) of the real number field
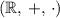 :
:
 .
.
 .
.
Note that this property features both addition and multiplication in the same equation. However, the equation in the question includes only addition. Therefore, this property would not apply here.
Associative Property
By the associative property of fields, for any three elements (
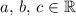 ) of the real number field
) of the real number field
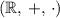 :
:
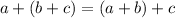 .
.
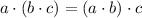 .
.
In particular, the equation
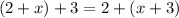 (where
(where
 ) illustrates the associative property of addition of the real number field.
) illustrates the associative property of addition of the real number field.
Note that even though the location of the parentheses have changed, the elements are still in the same place (with
 ,
,
 , and
, and
 in the same order on both sides of the two equations.)
in the same order on both sides of the two equations.)
Commutative Property
By the commutative property of fields, for any two elements (
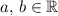 ) of the real number field
) of the real number field
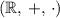 :
:
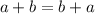 .
.
 .
.
The commutative property of fields allow the elements in the additions and in multiplications to be rearranged. (In contrast, the associative property allows for only the rearrangement of the parentheses.)
That doesn't apply to
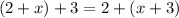 because the numbers and symbols appear in the same order on both sides of the equation.
because the numbers and symbols appear in the same order on both sides of the equation.