Question

Name the property of real numbers illustrated by the equation (2 + x) + 3 = 2 + (x + 3).

Identity Property


Distributive Property


Associative Property


Commutative Property

Answer 1

associative property

Explanation:

:)

Answer 2

This equation illustrates the associative property of the real number field,
`(\mathbb{R},\, +,\, \cdot)`.

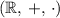Explanation:

All four choices here are indeed properties of the field of real numbers,
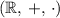`(\mathbb{R},\, +,\, \cdot)`. However, the equation
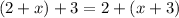`(2 + x) + 3 = 2 + (x + 3)` makes use of only the associative property.

Identity Property

By identity property of fields, the real number field
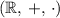`(\mathbb{R},\, +,\, \cdot)` should contain an identity element
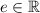`e \in \mathbb{R}`, such that for any element of that field
`a \in \mathbb{R}`:

`a + e = a`.

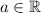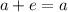In particular, the identity element of the real number field
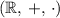`(\mathbb{R},\, +,\, \cdot)` is the real number
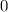`0`. The identity property (of addition) would then read:

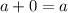`a + 0 = a` for any
`a \in \mathbb{R}`.

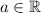Distributive Property

By the distributive property of fields, for any three elements (
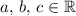`a,\, b,\, c \in \mathbb{R}`) of the real number field
`(\mathbb{R},\, +,\, \cdot)`:

`a\cdot (b + c) = a \cdot b + a \cdot c`.

`(a + b) \cdot c = a \cdot c + b \cdot c`.

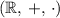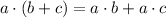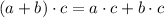Note that this property features both addition and multiplication in the same equation. However, the equation in the question includes only addition. Therefore, this property would not apply here.

Associative Property

By the associative property of fields, for any three elements (
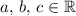`a,\, b,\, c \in \mathbb{R}`) of the real number field
`(\mathbb{R},\, +,\, \cdot)`:

`a + (b + c) = (a + b) + c`.

`a \cdot (b \cdot c) = (a \cdot b) \cdot c`.

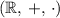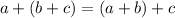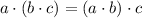In particular, the equation
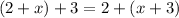`(2+ x) + 3 = 2 + (x + 3)` (where
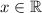`x \in \mathbb{R}`) illustrates the associative property of addition of the real number field.

Note that even though the location of the parentheses have changed, the elements are still in the same place (with
`a`,
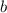`b`, and
`c` in the same order on both sides of the two equations.)

Commutative Property

By the commutative property of fields, for any two elements (
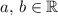`a,\, b\in \mathbb{R}`) of the real number field
`(\mathbb{R},\, +,\, \cdot)`:

`a + b = b + a`.

`a \cdot b = b \cdot a`.

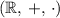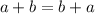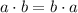The commutative property of fields allow the elements in the additions and in multiplications to be rearranged. (In contrast, the associative property allows for only the rearrangement of the parentheses.)

That doesn't apply to
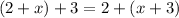`(2+ x) + 3 = 2 + (x + 3)` because the numbers and symbols appear in the same order on both sides of the equation.