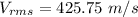Question

g the space in between two glass sheets has a volume of 0.025 m3. If the temperature of the gas is 290 K, what is the rms speed of the gas atoms

Answer 1

Complete Question

Argon gas (a monatomic gas) is sometimes used to insulate a double-pane window for purposes of insulation. In a particular window, the space in between two glass sheets has a volume of
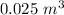`0.025 \ m^3`. If the temperature of the gas is 290 K. what is the rms speed of the gas atoms? The atomic mass of Argon is 39.9 u.(l u= 1.66x10-27 kg) Enter your answer in m/s

Answer:

The value is
`V_(rms) = 425.75 \ m/s`

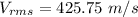
Step-by-step explanation:

From the question we are told that

The volume of the space in between the two glass sheet is
`a = 0.025 \ m^3`

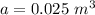
The temperature of the gas is
`T = 290 \ K`

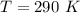
The atomic mass of Argon is
`m = 39.9 \ u = 39.9 * 1.66 *10^(-27) = 6.623 *10^(-26) \ kg`

Generally the root mean square velocity is mathematically represented as

`V_(rms) = \sqrt{(3 K T)/( m ) }`

Here K is the Boltzmann constant with value
`k = 1.38 *10^(-23) \ m^3 \cdot kg \cdot s^(-2) \cdot K^(-1)`

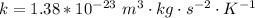
So

`V_(rms) = \sqrt{(3 * 1.38 *10^(-23) * 290 )/( 6.6234*10^(-26) ) }`

=>
`V_(rms) = 425.75 \ m/s`