Answer: (0, 1, 3)
Explanation:
- Adding the second and third equations, we get
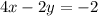
- Multiplying both sides of the first equation by 2, we get that
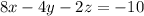 . Adding this to the second equation, we get that
. Adding this to the second equation, we get that
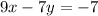 .
.
If we multiply both sides of the equation
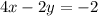 by 7, we get
by 7, we get
 .
.
If we multiply both sides of the equation
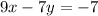 by 2, we get
by 2, we get
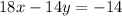 .
.
Subtracting the equation
 from the equation
from the equation
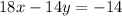 , we get that
, we get that
 .
.
This means that
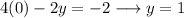
And thus,
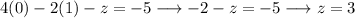 .
.
So, the solution is (0, 1, 3).