Question

Find all values of c in the open interval (a, b) such that f'(c)=(f(b)-f(a))/(b-a)

f(x)=4sin(x), [0,π]​

Answer 1

Answer: c = pi/2

There is only one value of c that satisfies the requirements.

=======================================================

Work Shown:

Let's compute the function value at the given endpoints of the interval.

`f(x) = 4\sin(x)\\\\f(\pi) = 4\sin(\pi) = 0\\\\f(0) = 4\sin(0) = 0\\\\`

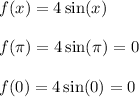
Which means,

`f'(c) = (f(b)-f(a))/(b-a)\\\\f'(c) = (f(\pi)-f(0))/(\pi-0)\\\\f'(c) = (0-0)/(\pi)\\\\f'(c) = (0)/(\pi)\\\\f'(c) = 0\\\\`

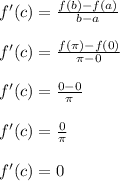
We want to find all values of c such that the derivative is 0.

This can be rephrased into wanting to solve
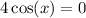`4\cos(x) = 0\\\\` since the derivative of sine is cosine

In other words,
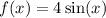`f(x) = 4\sin(x)\\\\` turns into
`f'(x) = 4\cos(x)\\\\`

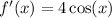
Solving that equation leads to:

`4\cos(x) = 0\\\\\cos(x) = 0\\\\x = (\pi)/(2)\\\\`

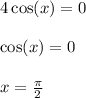
Use a reference table or the unit circle to determine this.

This is the value of c that satisfies f ' (c) = 0, such that
`0 < c < \pi`. No other value of c works.

If you graphed f(x) = 4sin(x), and only focused on the interval [0,pi], then you'll find that there's a horizontal tangent at the point (pi/2, 4). Note how the endpoints have the same y value so that's why the average rate of change over [0,pi] is 0.

Side note: this is an application of Rolle's Theorem