Since G is the centroid of triangle ABC, and AD is perpendicular to CB, the length of the segment include;
1. AG = 10 units.
2. GD = 5 units.
3. CD = 12 units.
4. GE = 6.5 units.
5. GB = 13 units.
In Mathematics and Geometry, the centroid theorem states that the centroid of a triangle is located at two-third (2/3) of the distance from the vertex to the midpoint of the (opposite) sides.
Part 1.
Based on the centroid theorem, we can logically deduce that point G represents the centroid of triangle ABC. If the length of AD is 15 units, the length of AG can be calculated as follows;
AG = 2/3 × AD
AG = 2/3 × 15
AG = 30/3
AG = 10 units.
Part 2.
For the length of GD, we have:
GD = AD - AG
GD = 15 - 10
GD = 5 units.
Part 3.
In order to determine the length of CD, we would apply Pythagorean's theorem;
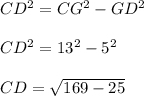
CD = 12 units.
Part 4.
If the length of CG is 13 units, the length of CE can be calculated as follows;
CG = 2/3 × CE
13 = 2/3 × CE
CE = 39/2
CE = 19.5 units.
Therefore, the length of GE is given by;
GE = CE - CG
GE = 19.5 - 13
GE = 6.5 units.
Part 5.
Based on the definition of a centroid, we can logically deduce the following congruent sides;
CG ≅ GB
CG = GB = 13 units.