Given:
The line contains the point (-5,-3) and has a slope of -2.
To find:
The graph of the line.
Solution:
The line contains the point (-5,-3) and has a slope of -2. So, the equation of line is
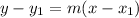
where, m is slope.
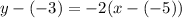
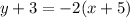
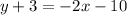
Subtracting 3 from both sides, we get
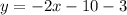
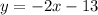
So, the equation of line is
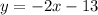 .
.
Putting x=0, we get
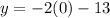
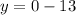
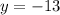
It means, the line also passes through (0,-13).
Plot the points (0,-13) and (-5,-3) on a coordinate plane and connect them by a straight line.
Therefore, the graph of given line is shown below.