Given:
LCM(a,b) = 90 and GCD(a,b) = 3.
b is three more than a.
To find:
The values of a and b.
Solution:
We have,
LCM(a,b) = 90
GCD(a,b) = HCF(a,b) = 3
According to the question,

If a and b are two positive integers, then
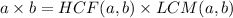
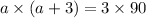
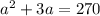

Splitting the middle terms, we get
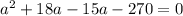
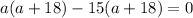
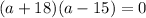
Using zero product property, we get
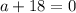 and
and
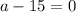
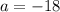 and
and
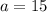
a is a positive integer so it cannot be negative. So, a=15.
Now,

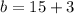

Therefore, the value of a is 15 and the value of b is 18.