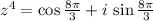Answer:
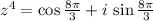
Explanation:
We can determine the power of a complex number by the De Moivre's Theorem, which states that for all
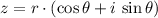 , where
, where
 , the power of the complex number is:
, the power of the complex number is:
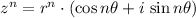 (1)
(1)
Where:
 - Magnitude of the complex number, dimensionless.
- Magnitude of the complex number, dimensionless.
 - Direction of the complex number.
- Direction of the complex number.
If we know that
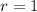 ,
,
 and
and
 , then the fourth power of the complex number is:
, then the fourth power of the complex number is:
![z^(4) = 1^(4)\cdot \left[\cos\left((8\pi)/(3) \right)+i\,\sin\left((8\pi)/(3)\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/d18v5n8qt1rqh28xgaisz88c1f4wnratid.png)