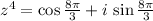Question

Suppose z = . What is z4?

on EDGE 2020

Answer 1

ITS B ON EDGE

Explanation:

Answer 2

`z^(4) = \cos (8\pi)/(3)+i\,\sin (8\pi)/(3)`

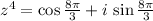
Explanation:

We can determine the power of a complex number by the De Moivre's Theorem, which states that for all
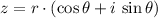`z = r\cdot (\cos \theta + i\,\sin\theta)`, where
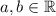`a, b \in \mathbb{R}`, the power of the complex number is:

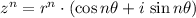`z^(n) = r^(n)\cdot (\cos n\theta + i\,\sin n\theta)` (1)

Where:

`r` - Magnitude of the complex number, dimensionless.

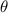`\theta` - Direction of the complex number.

If we know that
`r = 1`,
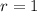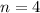`n = 4` and
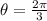`\theta = (2\pi)/(3)`, then the fourth power of the complex number is:

`z^(4) = 1^(4)\cdot \left[\cos\left((8\pi)/(3) \right)+i\,\sin\left((8\pi)/(3)\right)\right]`

`z^(4) = \cos (8\pi)/(3)+i\,\sin (8\pi)/(3)`