Question

Please help ASAP!!!

Chuck Stone is standing atop a high platform. He fires a rock up into the air with his slingshot. While it is in flight, the rock's distance in feet above the ground f(x) is a quadratic equation of time in seconds (x). This situation is modeled by the following function: f(x) = -5x^2 + 40x + 30.

a. How high above the ground is the platform?
30
b. How long does it take for the rock to hit the ground? Show all work to receive full credit!

is 30 correct for a? and please help me with b! Thank you!!!

Answer 1

a) the platform is 110 feet above the ground.

b) It takes 8.69 sec for the rock to hit the ground

Explanation:

This situation is modelled by the following function:
`f(x) = -5x^2 + 40x + 30\\`

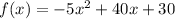
We need to answer the following questions.

a) How high above the ground is the platform?

First we find x using the formula:
`x=-(b)/(2a)`

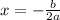
we have b = 40 and a = -5

Putting values and finding x

`x=-(b)/(2a)\\x=-(40)/(2(-5))\\x=-(40)/(-10)\\x=4`

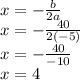
Now putting x=4 in the function to find how high above the ground is the platform

`f(x) = -5x^2 + 40x + 30\\Put\:x=4\\f(4)=-5(4)^2+40(4)+30\\f(4)=-5(16)+160+30\\f(4)=-80+160+30\\f(4)=110`

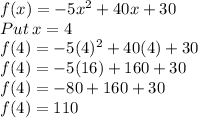
So, the platform is 110 feet above the ground.

b) How long does it take for the rock to hit the ground? Show all work to receive full credit!

We will factorise the given function
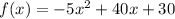`f(x) = -5x^2 + 40x + 30` to find the time taken to hit the ground.

We can solve the equation using quadratic formula:
`x=(-b\pm√(b^2-4ac))/(2a)`

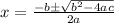
We have a =-5, b=40, c=30

Putting values and finding x

`x=(-b\pm√(b^2-4ac))/(2a)\\x=(-40\pm√((40)^2-4(-5)(30)))/(2(-5))\\x=(-40\pm√(1600+600))/(-10)\\x=(-40\pm√(2200))/(-10)\\x=(-40\pm46.9)/(-10)\\x=(-40+46.9)/(-10),x=(-40-46.9)/(-10) \\x=-0.69,x=8.69`

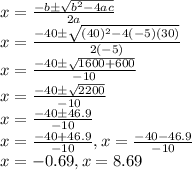
So, we get values of x: x = -0.69 and x=8.69

As time cannot be negative, so we take x=8.69

So, It takes 8.69 sec for the rock to hit the ground