Answer:
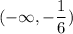
Explanation:
We have the function:
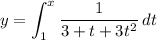
And we want to find the interval for which y is concave upwards.
Therefore, we will need to find the second derivative of y, find its inflection points (where y''=0), and test for values.
So, let's take the derivative of both sides with respect to x. So:
![\displaystyle y^\prime=(d)/(dx)\Bigg[\int_(1)^(x)(1)/(3+t+3t^2)\, dt\Bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/tnw9v7f014iykf56i8lwwec7roaai4krrp.png)
By the Fundamental Theorem of Calculus:

So, we will take the derivative again. Hence:
![\displaystyle y^\prime^\prime=(d)/(dx)\Big[(1)/(3+x+3x^2)\Big]=(d)/(dx)\Big[(3+x+3x^2)^(-1)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/tjum7kp1t7eiqcadfdbqguxqn8qnafkrqd.png)
We will use the chain rule. Let:
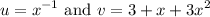
Differentiate:
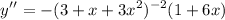
Rewrite:
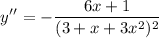
So, points of inflection, where the concavity changes, is whenever the second derivative is 0 or undefined.
We can see that the second derivative will never be undefined since the denominator can never equal 0.
So, our only possible inflection points are when it's equal to 0. Hence:
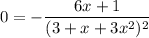
Multiplying both sides by the denominator gives:
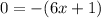
Then it follows that:
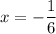
So, our only possible point of inflection is at x=-1/6.
We will test for values less than and greater than this inflection point.
Testing for x=-1, we see that:
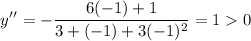
Since the result is positive, y is concave up for all values less than -1/6.
And testing for x=0, we see that:
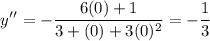
Since the result is negative, y is concave down for all values greater than -1/6.
Therefore, the interval for which y is concave up is:
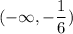
Note that we use parentheses instead of brackets since at exactly x=-1/6, our graph is neither concave up nor concave down.