Answer: 72 cubic inches
Explanation:
The formula for the volume of a cone:
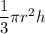
Formula for the volume of a cylinder:

We are given that a cylinder should fit exactly inside the cone
Upon comparing the two equations above, we get:

Since we are given the volume of cone is 24 cubic inches, we can write down the below:
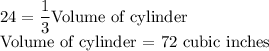
Therefore, we can conclude that if the volume of the cylinder is 72 cubic inches, then the cone with volume of 24 cubic inches can fit exactly in.