Question

a sphere with a radius of 8cm carries a uniform volume charge density of 1.5 find the magnitude of the electric field

Answer 1

E = 5.65 x 10¹⁰ N/C

Step-by-step explanation:

First we need to find the total charge on the sphere. So, we use the following formula for that purpose:

`q = \sigma V\\`

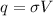
where,

q = total charge on sphere

V = Volume of Sphere =
`(4)/(3) \pi r^3 = (4)/(3) \pi (0.08\ m)^3 = 0.335\ m^3`

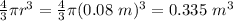
σ = volume charge density = 1.5 C/m³

Therefore,

`q = (0.335\ m^3)(1.5\ C/m^3) \\q = 0.502 C`

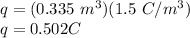
Now, we use the following formula to find the electric field due to this charged sphere:

`E = (kq)/(r^2)`

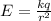
where.

E = Electric Field Magnitude = ?

k = Coulomb's Constant = 9 x 10⁹ N.m²/C²

r = radius of sphere = 8 cm = 0.08 m

Therefore,

`E = ((9\ x\ 10^9\ Nm^2/C^2)(0.502 C))/((0.08\ m)^2)\\\\`

E = 5.65 x 10¹⁰ N/C