Answer:
E = 5.65 x 10¹⁰ N/C
Step-by-step explanation:
First we need to find the total charge on the sphere. So, we use the following formula for that purpose:
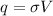
where,
q = total charge on sphere
V = Volume of Sphere =
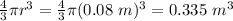
σ = volume charge density = 1.5 C/m³
Therefore,
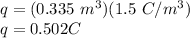
Now, we use the following formula to find the electric field due to this charged sphere:
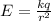
where.
E = Electric Field Magnitude = ?
k = Coulomb's Constant = 9 x 10⁹ N.m²/C²
r = radius of sphere = 8 cm = 0.08 m
Therefore,
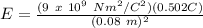
E = 5.65 x 10¹⁰ N/C