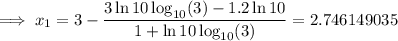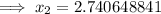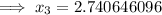Answer:
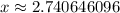
Explanation:
Given:
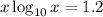
Rewrite so that it's equal to zero:
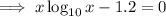
Therefore:
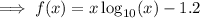
Differentiate the function:
Use the product rule to differentiate
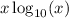 :
:
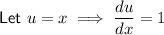
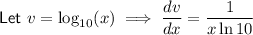
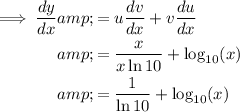
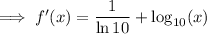
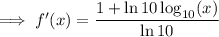
Newton-Rhapson iteration formula
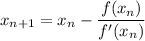
Substitute the function and its derivative into the formula, replacing x with
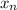 :
:
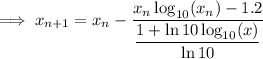
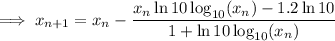
Therefore, the iteration formula is:
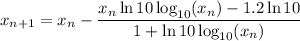
Let
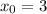
Substitute this into the formula and carry out 3 iterations: