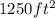Hey there mate ;)
Note that the quadratic function
A(x) = x(100-2x) gives the area.
Now, this equation is equivalent to:
A(x) = 100x - 2x²
To find maximum value of A, we first find the derivative of the given function:
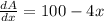
Now find the critical value by setting dA/dx=0, that is:-
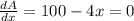
Solving for x, we get:
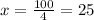
Hence, the critical point is x=25
Now, Find 2nd derivative to check if the equation has maximum value:
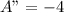
Noting that the 2nd derivative is negative, hence, we have a maximum value. Infact, the maximum value in this case is when the value of x = 25.
The maximum area is therefore,

→ The Correct answer is: