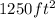Question

You are building a rectangular fenced in area for your pets to run around. You want your pet to have a maximum area to run around in and you have 100 feet of fence to work with. What are the dimensions for a maximum area?

Answer 1

Hey there mate ;)

Note that the quadratic function

A(x) = x(100-2x) gives the area.

Now, this equation is equivalent to:

A(x) = 100x - 2x²

To find maximum value of A, we first find the derivative of the given function:

`(dA)/(dx) = 100 - 4x`

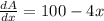
Now find the critical value by setting dA/dx=0, that is:-

`(dA)/(dx) = 100 - 4x = 0`

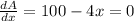
Solving for x, we get:

`x = (100)/(4) = 25`

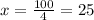
Hence, the critical point is x=25

Now, Find 2nd derivative to check if the equation has maximum value:

`A`

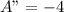
Noting that the 2nd derivative is negative, hence, we have a maximum value. Infact, the maximum value in this case is when the value of x = 25.

The maximum area is therefore,

`A = 25(100 - 2(25))`

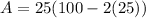
→ The Correct answer is:

`1250ft^(2)`