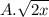When x>0, the expression
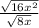 simplifies to
simplifies to
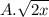 . The correct option is
. The correct option is
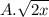 .
.
Let's simplify the expression
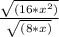
 can be simplified to 4x because the square root of 16 is 4 and
can be simplified to 4x because the square root of 16 is 4 and
 is x squared.
is x squared.
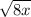 can be simplified as
can be simplified as
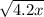 , which further simplifies to
, which further simplifies to
 because the square root of 4 is 2.
because the square root of 4 is 2.
Now, let's substitute these simplified forms back into the expression:
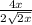
Simplifying the fraction by canceling out the common factor of 2 in the numerator and denominator gives:
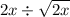
This can be rewritten as
 , which is equal to
, which is equal to
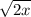 .
.
So, when x>0, the expression
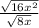 simplifies to
simplifies to