Answer:
C. 647 square units
Explanation:
To find the shaded area, subtract the area of the unshaded square from the area of the octagon.
Area of the octagon

where:
- n = number of sides
- l = length of one side
- a = apothem
Given:
Substitute the given values into the formula and solve for A:
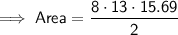
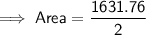
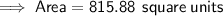
Area of the square
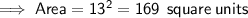
Area of the shaded region
= area of the octagon - area of the square
= 815.88 - 169
= 646.88
= 647 square units (nearest square unit)