Answer:
The expression to represent the length
Explanation:
Given
We know that The formula for the area of the rectangle is:
Thus, the length of a rectangle
Length = Area ÷ Width
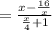
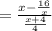
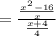
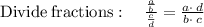
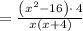
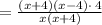
Cancel the common factor: (x+4)
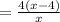
Thus, the expression to represent the length