Question

the area of a rectangle is x-16/x. If the width of a rectangle is x/4+1, find an expression to represent the length.

Answer 1

The expression to represent the length

• 
  `length=(4\left(x-4\right))/(x)`

Explanation:

Given

• Area = x-16/x

• Width = x/4+1

• Length =?

We know that The formula for the area of the rectangle is:

• Area = Length x Width

Thus, the length of a rectangle

Length = Area ÷ Width

`=(x-(16)/(x))/((x)/(4)+1)`

`=(x-(16)/(x))/((x+4)/(4))`

`=((x^2-16)/(x))/((x+4)/(4))`

`\mathrm{Divide\:fractions}:\quad ((a)/(b))/((c)/(d))=(a\cdot \:d)/(b\cdot \:c)`

`=(\left(x^2-16\right)\cdot \:4)/(x\left(x+4\right))`

`=(\left(x+4\right)\left(x-4\right)\cdot \:4)/(x\left(x+4\right))`

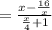
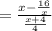
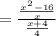
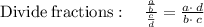
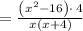
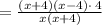
Cancel the common factor: (x+4)

`=(4\left(x-4\right))/(x)`

Thus, the expression to represent the length

• 
  `length=(4\left(x-4\right))/(x)`