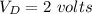Answer:
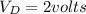
Step-by-step explanation:
First we need to find the value of diode current:
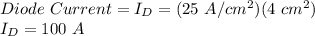
Now, we use ideal diode equation:
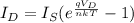
where,
Is = saturation current = 2 x 10⁺¹⁵ A
q = charge on electron = 1.6 x 10⁻¹⁹ C
V_D = Diode Voltage = ?
n = ideality factor = 1 (for ideal diodes)
k = Boltzman constant = 1.38 x 10⁻²³ J/k
T = Temperature = 300 k
Therefore,
![100\ A = (2\ x\ 10^(-15)\ A)(e^{[(1.6\ x\ 10^(-19) C\ V_(D))/((1)(1.38\ x\ 10^(-23))(300\ k))]}-1)\\\\(100\ A)/(2\ x\ 10^(-15)\ A) = e^{[(38.64 V^(-1))(V_(D))]}-1](https://img.qammunity.org/2021/formulas/physics/high-school/ksgnf6gpld2g4i95xf58r3dby3b3imkpou.png)
taking natural log on both sides:
![ln(5\ x\ 10^(16)) = ln[e^{(38.6\ V^(-1)\ V_(D))} - 1]\\38.45 = (38.6\ V^(-1))(V_(D)) - 1\\\\V_(D) = (38.45)/(38.6\ V^(-1)) + 1\\\\](https://img.qammunity.org/2021/formulas/physics/high-school/do0k2uert7w3q0dq3v27tknc0qbn5tpxcp.png)