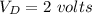Question

Use the ideal diode equation to calculate the voltage required to produce a current density of 25 A/cm2 for a junction of cross-sectional area 10-4 cm2, a reverse saturation current of 2x10-15 A and at 300 K

Answer 1

`V_(D) = 2 volts`

Step-by-step explanation:

First we need to find the value of diode current:

`Diode\ Current = I_(D) = (25\ A/cm^2)(4\ cm^2)\\I_(D) = 100\ A`

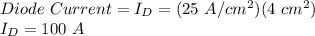
Now, we use ideal diode equation:

`I_(D) = I_(S)(e^{(qV_(D))/(nkT)}-1)\\`

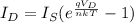
where,

Is = saturation current = 2 x 10⁺¹⁵ A

q = charge on electron = 1.6 x 10⁻¹⁹ C

V_D = Diode Voltage = ?

n = ideality factor = 1 (for ideal diodes)

k = Boltzman constant = 1.38 x 10⁻²³ J/k

T = Temperature = 300 k

Therefore,

`100\ A = (2\ x\ 10^(-15)\ A)(e^{[(1.6\ x\ 10^(-19) C\ V_(D))/((1)(1.38\ x\ 10^(-23))(300\ k))]}-1)\\\\(100\ A)/(2\ x\ 10^(-15)\ A) = e^{[(38.64 V^(-1))(V_(D))]}-1`

taking natural log on both sides:

`ln(5\ x\ 10^(16)) = ln[e^{(38.6\ V^(-1)\ V_(D))} - 1]\\38.45 = (38.6\ V^(-1))(V_(D)) - 1\\\\V_(D) = (38.45)/(38.6\ V^(-1)) + 1\\\\`

`V_(D) = 2\ volts`