Answer:
Alice started with $30
Explanation:
Understanding the situation
There are 3 steps to the transactions:
- the initial amounts, (before any transfers)
- the amounts after Alice first gives Bob money, and
- the amounts after Bob gives Alice some money back.
Organizing the variables
For organizational purposes, let's create variables for each person for each stage of the transaction, variables "a" for Alice, and "b" for Bob, with subscripts to denote which stage of the process we're talking about. For instance,
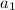 is the amount Alice has at step 1 (before any transfers), and
is the amount Alice has at step 1 (before any transfers), and
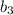 is the amount Bob has after Bob gives Alice some money back at the end.
is the amount Bob has after Bob gives Alice some money back at the end.
Translating the sentences into equations
"Alice gave Bob as many dollars as Bob had."
This means that the magnitude of the change for Alice between her Step 1 and Step 2 was equal to the amount Bob had at the beginning (Step 1):
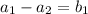
This also means that Bob's money in Step 2 increased to double what it used to be in Step 1:

"Bob then gave Alice as many dollars Alice then had."
Similar to the last sentence, this means that the magnitude of the change for Bob between Step 2 and Step 3 was equal to the amount Alice had at Step 2:
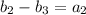
It also means that Alice's money in Step 3 increased to double what it used to be in Step 2:

"At this point, each had 24 dollars"
This means that both people had 24 dollars at Step 3:
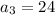 and
and
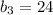
"How much did Alice have at the beginning?"
Solve for
Solving the system of equations
We effectively have a system of 6 equations and 6 unknowns. To solve this system, we'll be using substitution. For ease of explanation, I'll number the equations below:
Eq1:
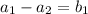
Eq2:

Eq3:
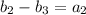
Eq4:

Eq5:
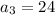
Eq6:
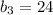
Substitute Eq6 (
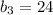 ) into Eq4
) into Eq4
Eq4:

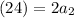
divide by 2
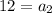 ***(we'll need this later)
***(we'll need this later)
Substitute this (
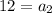 ) and Eq5 (
) and Eq5 (
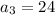 ) into Eq3
) into Eq3
Eq3:
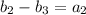

add 24
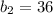
Substitute this (
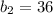 ) into Eq2
) into Eq2
Eq2:


Divide by 2
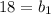
Substitute this (
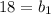 ) and ***(
) and ***(
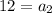 ) into Eq1:
) into Eq1:
Eq1:
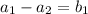
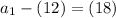
Add 12
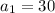
So, Alice had 30 dollars at Step 1, before she gave any to Bob.