Question

Eliza reads \large \frac{1}{7} of her book on Monday. On Tuesday and Wednesday combined, she reads three times as much as she reads on Monday. The expression \large \frac{1}{7}r+3\left(\frac{1}{7}r\right)can be used to determine the nubmer of pages Eliza reads on Monday, Tuesday, and Wednesday combined. The variable r represents the total number of pages in the book.

Answer 1

Eliza reads a total of 204 pages in the three days combined.

Explanation:

From the given information, we are being told that:

Eliza reads
`(1)/(7)` of her book on Monday.

On Tuesday and Wednesday combined, she reads thrice as much as she read on Monday.

Let assume that; Tuesday = T and Wednesday = W

Then;

`T + w = 3 ( (1)/(7))`

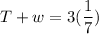
The expression to determine the total number of pages is given as:

`\large (1)/(7)r+3\left((1)/(7)r\right)`

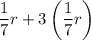
where;

r = total number of pages in the book.

Assuming that Eliza book contains a total of 357 pages. How many pages does she read in the three days combined together.

i.e.

r = 357

Then;

`\implies \large (1)/(7)(357)+3\left((1)/(7)(357)\right)`

`\implies 51+3(51))`

`\implies 51+153`

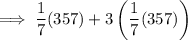
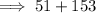
= 204 pages

Thus, Eliza reads a total of 204 pages in the three days combined.