Question

Which one of the following suggests that the data set is approximately​ normal?

a. A data set with ​14, ​68, and s41.
b. A data set with ​1330, ​2940, and s2440.
c. A data set with ​2.2, ​7.3, and s2.1.
d. A data set with ​105, ​270, and s33.

Answer 1

a. A data set with ​14, ​68, and s41.

Explanation:

For a normally distributed data set; Q₁ and Q₃ will be 0.6745 × 2 = 1.349 standard deviation.

The interquartile range IQR = Q₃ - Q₁ = 1.349 ×
`{\sigma}`

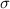
Q₁ Q₃
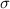`{\sigma}` IQR = Q₃ - Q₁ 1.349 ×
`{\sigma}`

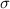
a. 14 68 41 = 68 - 14 1.349 × 41

= 54 = 55.309

b. 1330 2940 2440 = 2940 - 1330 1.349 × 2440

= 1610 = 3291.56

c. 2.2 7.3 2.1 = 7.3 - 2.2 1.349 × 2.1

= 5.1 = 2.8329

d. 105 270 33 = 270 - 105 1.349 × 33

= 165 = 44.517

From the above calculation, we will see that option a have a data set that is approximately normal.