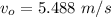Answer:
The value is
Step-by-step explanation:
From the question we are told that
The emitted frequency increased by
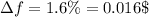
Let assume that the initial value of the emitted frequency is

Hence new frequency will be
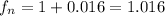
Generally from Doppler shift equation we have that
![f_1 = [( v \pm v_o)/(v \pm + v_s ) ] f](https://img.qammunity.org/2021/formulas/physics/college/njut5f38f23jqy2mo9mytgy4mqurxa32t2.png)
Here v is the speed of sound with value
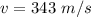
 is the velocity of the sound source which is
is the velocity of the sound source which is
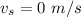 because it started from rest
because it started from rest
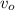 is the observer velocity So
is the observer velocity So
Generally given that the observer id moving towards the source, the Doppler frequency becomes
![f_1 = [( v + v_o)/(v + 0 ) ] f](https://img.qammunity.org/2021/formulas/physics/college/oeq29b6eb9ifa8gv6doi9ropb25tdtji8f.png)
=>
![1.016 = [( 343 + v_o)/(343 ) ] * 1](https://img.qammunity.org/2021/formulas/physics/college/5usx65zx62qk22ciqa20sy7gdopfcqjdpl.png)
=>