Question

A 3.00 kg mass is pushed against a spring and released. If the spring constant of the

spring is 7500 N/m and the spring is compressed 10.0 cm:
i. What is the energy stored in the compressed spring? [2 points]
ii. What is the maximum speed
`⃗_(0)` of the mass? [2 points]
iii. The mass then travels across a rough surface and then up a smooth ramp. The speed
at the beginning of the ramp is ⃗1 = 4.00 m/s. What is the work done by friction as
the mass moves across the rough surface? [2 points]
iv. The block then travels up the smooth ramp and continues on vertically. How high
does it go? [2 points]

Answer 1

Energy stored in the compressed spring:
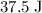`37.5\; \rm J` before the mass is released.

Maximum horizontal speed of the mass:
`5.0\; \rm m \cdot s^(-1)`.

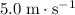(Assumption: the surface between the mass and the ground is frictionless until the mass separates from the spring.)

(Maximum horizontal acceleration of the mass:
`250\;\rm m \cdot s^(-2)`.)

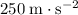Work that friction did on the mass:
`13.5\; \rm J`.

Maximum height of the mass: approximately
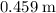`0.459\; \rm m` (assuming that
`g = 9.8\; \rm m \cdot s^(-2)`.)

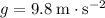Step-by-step explanation:

Energy stored in the spring

When an ideal spring of spring constant
`k` is compressed by a displacement of
`x` from the equilibrium position, the elastic potential energy stored in the spring is:

`\displaystyle (1)/(2)\, k \cdot x^(2)`.

The question states that for this spring,
`k = 7500\; \rm N \cdot m^(-1)` (Newtons per meters) whereas
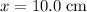`x = 10.0\; \rm cm` (centimeters.) Convert the unit of
`x` to meters to match the unit of
`k`:

`\begin{aligned} x &= 10.0\; \rm cm\\ &= 10.0\; \rm cm * (1\; \rm m)/(100\;\rm cm) = 0.100\; \rm m\end{aligned}`.

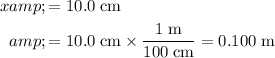Calculate the energy stored in this spring:

`\begin{aligned}& \text{Elastic Potential Energy} \\ &= (1)/(2)\, k \cdot x^(2) \\ &= (1)/(2) * 7500\; \rm N \cdot m^(-1) * 0.100\; \rm m \\ &=37.5\; \rm J \end{aligned}`.

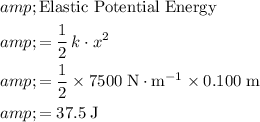Maximum horizontal speed of the mass

Assume that the surface under the spring is frictionless. All that
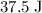`37.5\; \rm J` of elastic potential energy would be converted to kinetic energy by the time the mass separates from the spring.

The horizontal speed of the mass is largest at that moment. The reason is that immediately after this moment, friction (between the surface and the mass) would start to slow the mass down immediately.

Calculate the speed
`v` of the mass
`m` at that moment.

`\displaystyle \text{Kinetic Energy} = (1)/(2)\, m \cdot v^(2)`.

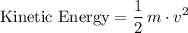Therefore:

`\displaystyle v = \sqrt{\frac{2\cdot (\text{Kinetic Energy})}{m}}`.

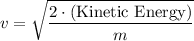The question states that
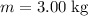`m =3.00\; \rm kg`. At that moment, the kinetic energy of the mass is
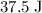`37.5\; \rm J` (or equivalently,
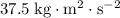`37.5\; \rm kg\cdot m^(2) \cdot s^(-2)` in base units.)

Calculate the speed of the mass at that moment from the kinetic energy of the mass:

`\begin{aligned}v &= \sqrt{\frac{2\cdot (\text{Kinetic Energy})}{m}} \\ &= \sqrt{(2 * 37.5\; \rm kg \cdot m^(2)\cdot s^(2))/(3.00\; \rm kg)} = 5.00\; \rm m \cdot s^(-1)\end{aligned}`.

Work friction did on the mass

Assume that the rough surface is level. Therefore, all the energy loss of the mass should be attributed to friction.

Kinetic energy of the mass before coming onto that rough surface:
`37.5 \; \rm J`.

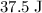Kinetic energy of the mass before leaving the rough surface:

`\begin{aligned} &(1)/(2)\, m \cdot v^(2) \\ &= (1)/(2) * 3.00\; \rm kg * {\left(4.00\; \rm m \cdot s^(-1)\right)}^(2) \\ &= 24.0\; \rm J \end{aligned}`.

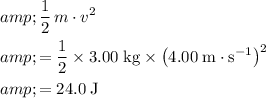If that rough surface is level, there would be no change to the gravitational potential energy of the mass. Calculate the change to the kinetic energy of the mass:

`37.5\;\rm J - 24.0\; \rm J = 13.5\; \rm J`.

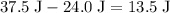That should be equal to the size of the work that friction did on the mass.

Maximum height of the mass

Assume that the smooth ramp does not change the total energy of the block. Therefore, the total mechanical energy of the block would still be
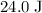`24.0\; \rm J` when the height of the block is maximized. However, all that energy would be in the form of gravitational potential energy.

Let
`g` denote the gravitational field strength (
`g \approx 9.8\; \rm m \cdot s^(2)`near the surface of the earth.) The gravitational potential energy of an object of mass
`m` and height
`h` (relative to the surface of zero gravitational potential energy) would be:

`\begin{aligned}&\text{Gravitational Potential Energy} = m \cdot g \cdot h\end{aligned}`.

Rewrite this equation to find an expression for
`h`:

`\displaystyle h = \frac{\text{Gravitational Potential Energy}}{m\cdot g}`.

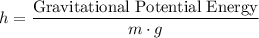Assume that
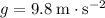`g = 9.8\; \rm m \cdot s^(-2)`. The question states that
`m = 3.00\; \rm kg`.
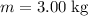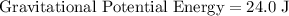`\text{Gravitational Potential Energy} = 24.0\; \rm J`. Therefore:

`\begin{aligned} &h\\ &= \frac{\text{Gravitational Potential Energy}}{m\cdot g}\\ &= (24.0\; \rm kg \cdot m^(2) \cdot s^(-2))/(3.00\; \rm kg * 9.8\; \rm m \cdot s^(-2)) \approx 0.459\; \rm m\end{aligned}`.